あなたは次の筆算を正しく計算できますか?
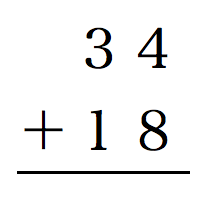
もちろんできますよね。
2桁同士の足し算は小学校2年生で習う問題ですから、このブログを見る人ならだれでもできるはずです。
しかし、次のように計算していませんか?
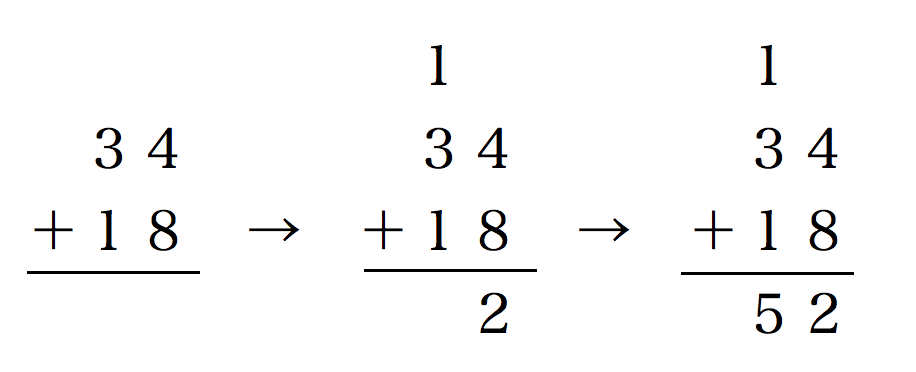
社会人になってもこのような計算をしているとしたら、あなたは優等生すぎるかもしれません。
なぜならば、小学校2年生で習った教科書通りの解き方をしています。
もしあなたが、学生生活を終え、社会人となっているのでしたら、次の計算方法の方が、合理的かもしれません。
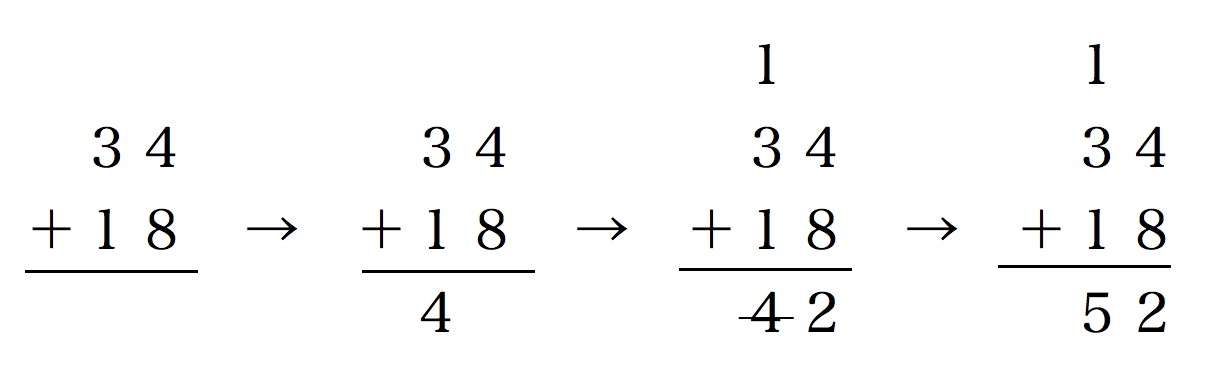
この二つの方法はどこが違うのでしょうか?
先ほどの方法は、1の位から計算をしました。今度の方法は10の位から計算しました。
繰り上がりの処理のために、後者の方が一手間ふえているのになぜ合理的なの?と思う方もいるかもしれません。
理由は、後者の方は途中でやめても、おおよその答えがわかるからです。
実社会において、精度が求められる計算は、コンピュータ、パソコンや電卓がやってくれます。
人が計算する時は、精度が求められる計算よりは、概算を早く求めるという状況の方が圧倒的に多いと思います。
例えば、財布の中のお金があまりなくて、スーパーで買い物をするとき、買い物カゴに入れながら、買いすぎないように計算をするはずです。
このとき、1の位から計算するのでは、「木を見て森を見ず」。
手間ばかりかかって、全体像がつかめません。
一方で、一番上位の1桁だけでも計算していけば、簡単におおよその金額はつかめるでしょう。
このように、一つの計算方法が常に正しいということはあまりなく、ケースによって、計算方法を変えるということが大切です。
コンピュータサイエンスでは、アルゴリズムを学びますが、筆算の方法も列記としたアルゴリズムです。
小学校2年生で習う方法と上の桁から計算する方法、どちらもアルゴリズムです。
2020年からの小学校でのプログラミング教育必修化でどのようなことを教えるのかはわかりませんが、
物事の解決方法にはいろいろな方法があるということを、コンピュータを通じて学ぶのもプログラミング教育の使命ではないでしょか?
(文:一般社団法人キッズITインストラクター協会 代表理事 棚橋一也)



